Diving Deeper - Real Application 🧐

Let’s go over the process of discovering weights step by step and in more detail to ensure you grasp the idea well before leveling up.

Step 0: Set the Goal

➡️Predict If a Post will go viral on Twitter (X) based on multiple factors (conditions).

Step 1: Collect Data

We will collect some data on already published posts. We want both viral posts and nonviral.

We will have something like this:

Hour of Day	Content Length	Engagement Score	Actual Virality
10	51	41.80	0
4	764	34.89	1
14	892	47.12	0
16	575	38.52	1
22	196	5.94	1

• Hour of Day: This will be an integer ranging from 0 to 23, representing the 24 hours in a day.
• Content Length: This can be an integer representing the number of characters in the post. Let's consider a range from 50 to 1000 characters.
• Engagement Score: This could be a floating-point number representing likes, shares, comments, etc., on a scale of 0 to 100.
• Virality: If a post is viral, it is 1. If not, it is 0.

How do we collect this data?

Great question! The way we collect data for a project like this is very important and can be done in several ways. We will dive deeper into the details of data collection methods later in this book. But to give you a quick overview:

• Manual Collection: In our scenario, This involves directly observing and recording data from social media posts. It's time-intensive but can be very accurate for specific needs.

• Using APIs: Social media platforms often provide Application Programming Interfaces (APIs), which are tools that allow us to automate the collection of large amounts of data.

• Web Scraping: This method uses software and scripts to extract data from websites and social media platforms automatically. It's useful for collecting data that isn't readily accessible via APIs.

• Public Datasets: Utilizing datasets released by government agencies, research institutions, or organizations, which can include social media data or related information.

Each method has its unique strengths and limitations. The choice of method depends on the project's specific needs, the resources available, and the type of data required for the analysis. Don’t bother your head about how we got the data now. Let’s focus on our project.

We just collected it in some way 🕵️

Step 2: Adjusting Numbers - Normalization

Let’s zoom in and look again at our data. I picked two records:

Hour of Day	Content Length	Engagement Score	Actual Virality
10	51	41.80	0
4	764	34.89	1

The hour of the day ranges from 0 to 23, while content length can range from 50 to 1000 or more. The Engagement Score can also range from 0 to 100.

So, we noticed that we have very different scales for each condition.

So we notice that we have very different scales for each condition.

These different ranges and scales can directly affect the weight calculation process simply because** the machine learning program might incorrectly assume that the condition with a larger range (like the content length) is more important! **

Here comes the idea of Normalization, or adjusting the numbers into a similar scale or range.

Think of it like converting different currencies into one common currency to compare their values easily. Just as you would convert dollars and euros into a single currency to compare their values, normalization converts all features into a common scale.

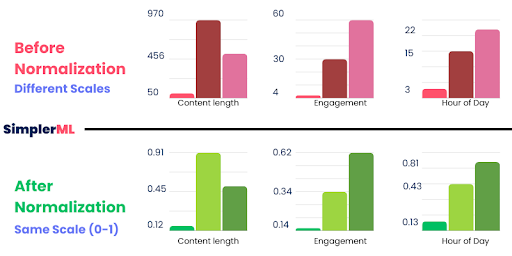
How to Apply Normalization?

There are several methods to normalize data, but one common method is Min-Max normalization.

It rescales the values to a range of 0 to 1. Here is how:

Let’s say we are normalizing the "Content-Length" of a post.

And take the second post in our dataset as an example.

The original content length for this post was 764 characters.

Now, we find the Minimum (Min) and Maximum (Max) Values for content length in the Dataset:

In our case:

Minimum = 51

Maximum = 892

If you go back to the table, you will see that I colored it red and blue.

Ok, now we can calculate the normalized value of Content-Length using the min-max method as follows:

(Original Value - Minimum) / (Maximum - Minimum)

If you prefer Mathematical Formulas, here we are:

$$\text{NormalizedValue} = \frac{\text{CurrentValue} - \text{MinimumValue}}{\text{MaximumValue} - \text{MinimumValue}}$$

Whatever you prefer, let's just apply this 3rd-grader formula to our numbers:

764 − 51 / 892 − 51 = 0.848

So 0.848 is the normalized ( scaled ) value.

If we repeat the operation on all values in our data. Our dataset is transformed as follows:

Hour of Day	Content Length	Engagement Score	Actual Virality
0.33	0.00	0.87	0
0.00	0.85	0.70	1
0.56	1.00	1.00	0
0.67	0.62	0.79	1
1.00	0.17	0.00	1

In this normalized dataset:

• The "Hour of Day" values range from 0 (representing the earliest hour in our dataset) to 1 (the latest hour).
• The "Content Length" values are scaled between 0 (shortest content) and 1 (longest content).
• The "Engagement Score" is also adjusted to a 0 to 1 scale, with 0 being the lowest engagement and 1 the highest.

Note that we will discuss data processing and normalization in more detail later in the book and with many more examples, but I tried here to introduce the concept with a real practical example.

Let’s continue!

Step 3: Initialize a random set of weights.

As we mentioned before, we will try to guess the weights! So, we will assume a set of weights between 0 and 1!

Let’s say:

• 0.71 for Hour of Day
• 0.82 for Content Length
• 0.11 for Engagement Score

Great! We have some weights we can test with.

---

Step 4: Predicting Popularity

Now that we have our normalized data and initial random weights, it's time to see how well these weights predict a post's popularity.

To illustrate this, consider the prediction as a straightforward calculation.

Each characteristic of a post (like the hour of the day, content length, and engagement score) is multiplied by its corresponding weight, which we had assumed randomly earlier.

The results of these multiplications are then summed up to yield a prediction score for each post.

For example, let's take the second post in our dataset and apply our weights to its characteristics:

Hour of Day Weight (0.71) × Hour of Day Score (0.00) + Content Length Weight (0.82) × Content Length Score (0.85) + Engagement Score Weight (0.11) × Engagement Score (0.70)

0.71 X 0.00 + 0.82 X 0.85 + 0.11 X 0.70 = 0.774

This score, 0.774 in our example, is our predicted popularity score for this particular post.

Now, we just repeat the same process on all posts. We get something like this:

• First Record: Popularity Score = 0.33
• Second Record: Popularity Score ≈ 0.774
• Third Record: Popularity Score ≈ 1.328
• Fourth Record: Popularity Score ≈ 1.071
• Fifth Record: Popularity Score ≈ 0.849

Perfect! We now have a list containing all the predicted popularity scores for each post.

---

Step 5: Measuring the Accuracy of Our Predictions

After predicting the popularity score for all posts, the next crucial step is to check how accurate this prediction is. To do this, we compare our prediction scores with a pre-set threshold that defines what we consider as 'viral.'

Let's set a simple rule for our predictions:

If a post's predicted score is higher than 0.85, we will classify it as viral.

This threshold is a value we decide on based on our understanding of what constitutes a viral post.

This threshold is a value we decide on based on our understanding of what constitutes a viral post.

In our example, the predicted score for the second post is 0.774. Since this score is lower than our threshold of 0.85, we predict that this post will not go viral.

But! If we look into our dataset, we see that this post is actually Viral! So, we conclude that our prediction is wrong, which means our weights are wrong!

So we have an error.

Calculate Post Prediction Error

To calculate this error for each post prediction, we go through the following steps:

1- Classify each prediction as 0 or 1 based on the predicted score and threshold

We then classify each post as viral (1) or not viral (0) by comparing its predicted score to the predefined threshold (e.g., 0.85)

• If the score is equal to or higher than the threshold, the post is classified as viral (predicted virality = 1).

• If the score is lower than the threshold, the post is classified as not viral (predicted virality = 0).

2- Calculating The Error

In our dataset, we compare each post's predicted virality (1 or 0) to its actual virality status (also 1 or 0).

The error for each post is the absolute difference between these two values:

• If the predicted virality matches the actual status (both 1 or both 0), the error is 0 (no error).
• If the predicted virality does not match the actual status (one is 1, and the other is 0), the error is 1 (misclassification).

Example 1: back to the second post:

Hour of Day	Content-Length	Engagement Score	Actual Virality
0.00	0.85	0.70	1

• Predicted Score = 0.774 (less than 0.85) → Predicted Virality = 0
• Actual Virality Value = 1
• Error = 1 (misclassification: 1-0 )

Example 2: Let’s Check Post number 4 in the table:

Hour of Day	Content-Length	Engagement Score	Actual Virality
0.67	0.62	0.79	1

• Predicted Score = 1.071 (greater than 0.85) → Predicted Virality = 1
• Actual Virality Value = 1
• Error = 0 (correct classification 1-1)

So in this way, we get the errors for all posts in our dataset.

3- Average Error Calculation:

Now, let's calculate the average error:

Average Error = Sum of All Errors / total number of posts

In our case:

0+1+1+0+0 / 5 = 2/5 = 0.4

So, the Average Error in our dataset for the assumed Weights is 0.4

Step 6: Calculating the Total Prediction Error

Okay, now we have the average error for our assumed weights, but the journey doesn’t end here. It is time to evaluate our guess (our assumed weights): Are they good or bad?

This is where the concept of an Error Threshold comes into play. Think of this threshold as a benchmark for performance. The closer we are to this number, the better our guess is.

In our case, we will set the error threshold to 0.2.

So, we will compare the Calculated Average Error (0.4) from step 5 with our predefined Error Threshold (0.2) now.

• If the average error is less than or equal to the Error Threshold, it means our model's predictions are somehow accurate, and the weights are acceptable.
• If the average error is greater than the Error Threshold, it indicates that our model's predictions are NOT accurate enough, and we need to adjust the weights.

In our example, it is 0.4 > 0.2

It means our guess is not up to the mark. Hence, we cannot accept these weights!

Step 7: Repeat with a new guess!

What now?

Simply start with a new guess and go again from step 3 to step 6 till we find a set of weights that works.

At that moment, we can congratulate ourselves on finding our lock's secret key combination! To be more accurate, we found a set of acceptable weights that can help us achieve our primary goal.

What was the main goal?! ➡️ Predict If a Post will go viral on Twitter (X)